2. Long-Lived Domain Wall Plasmons in Gapped Bilayer Graphene

Paper ini adalah paper yang ditulis oleh kolega saya, Dr. Eddwi Heski Hasdeo, mengenai plasmon yang terlokalisasi pada sisi dari material dua dimensi. Plasmon ini disebut sebagai edge plasmon (EP). Dalam studi ini, penulis membahas EP yang berada pada batas antara dua region yang memiliki tanda dari gap energi yang berlawanan. Batas ini disebut sebagai domain wall states. Berdasarkan hasil perhitungan, EP pada domain wall states memiliki waktu hidup (lifetime) yang panjang dibandingkan dengan plasmon permukaan (surface plasmon) konvensional.

Edge Plasmon dengan waktu hidup yang panjang

Plasmon adalah eksitasi kolektif dari elektron, di mana rapat elektron berosilasi bersamaan secara kolektif dalam suatu material logam. Pada permukaan logam tersebut, rapat elektron mengalami diskontinuitas, maka rapat elektron dapat terlokalisasi pada permukaan. Karena lokalisasi ini, rapat elektron dapat berosilasi secara kolektif pada permukaan logam. Osilasi rapat elektron ini disebut sebagai plasmon permukaan. Selain memiliki komponen medan listrik yang searah dengan arah osilasi (longitudinal), plasmon permukaan juga memiliki komponen medan listrik yang tegak lurus terhadap arah osilasi (transversal), maka plasmon permukaan dapat dieksitasi menggunakan cahaya.

Definisi permukaan adalah batas antara dua media yang berbeda, seperti permukaan logam dengan udara. Batas ini dapat menyebabkan diskontinuitas dari rapat elektron. Semisal kita memiliki material dua dimensi, seperti graphene, maka selain permukaan graphene itu sendiri, kita juga memiliki sisi dari graphene juga sebagai batas antara graphene dengan udara. Karena adanya sisi ini, maka rapat elektron dalam graphene akan terlokalisasi di dekat sisi graphene. Jenis plasmon permukaan ini dinamakan dengan edge plasmon (EP) atau plasmon sisi. EP berosilasi pada sepanjang sisi graphene dengan potensial listrik yang meluruh sebagai fungsi jarak dari sisi. EP juga memiliki energi yang lebih rendah dari pada plasmon permukaan graphene.

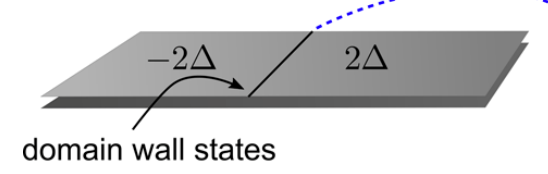
Mengapa kita membahas EP? Berdasarkan hasil perhitungan dari Hasdeo et al., EP dapat memiliki waktu hidup (lifetime) yang lebih panjang daripada plasmon permukaan. Selain itu, bila material dua dimensi tersebut memiliki konduktivitas Hall, maka EP menjadi chiral, yang berarti kecepatan EP menjalar ke kanan dan ke kiri tidaklah sama. Hasdeo et al membahas EP pada batas dari dua material yang memiliki tanda dari gap energi yang berlawanan seperti gambar di bawah. Tanda dari gap energi berkaitan dengan topologi dari suatu material dua dimensi dan bila dua material dengan tanda gap energi yang berlawanan dihubungkan, maka akan muncul edge states pada batas antara dua material tersebut, di mana rapat electron terlokalisasi di batas dua material. Bila energy Fermi berada pada gap energi, material tetap bersifat logam, tetapi hanya pada batas dua material saja, sehingga EP masih dapat menjalar meskipun pada permukaan material (tidak pada sisi) tidak ada rapat elektron karena bersifat insulator.

Bagaimana cara kita membuat tanda gap energi yang berlawanan? Salah satu cara adalah dengan menggunakan dua gate voltage pada satu permukaan bilayer graphene. Bila kita mengaplikasikan gate voltage pada permukaan bilayer graphene, gap energi akan muncul yang tandanya bergantung pada tanda dari gate voltage itu sendiri. Jadi bila ada dua gate voltage pada permukaan bilayer graphene, maka kita dapat membuat dua region, di mana tanda gap energi nya berlawanan (-2Δ dan 2Δ ) dan edge states dapat muncul pada batas kedua region ini seperti gambar di atas. Edge states ini diberi nama domain wall states.

EP dimodelkan sebagai gelombang yang menjalar pada sisi graphene. Semisal sisi berada pada koordinat x = 0, maka potensial listrik ϕ dan rapat elektron δρ dari EP dapat dimodelkan sebagai berikut,

Di mana fungsi delta Dirac pada δρ menunjukkan bahwa elektron berada di permukaan graphene. Besarnya amplitudo potensial dapat diperoleh dengan menyelesaikan persamaan Poisson sebagai berikut,

Dengan mensubstitusikan persamaan (1) dan (2) ke (3) dan melakukan penyederhanaan, maka kita mendapatkan persamaan berikut,

Di mana kita fokus pada potensial listrik EP pada permukaan graphene z = 0. Dengan menggunakan persamaan kontinuitas muatan dan juga persamaan kondisi batas untuk potensial listrik (di mana potensial listrik kontinu pada sisi dan turunan dari potensial listrik menjadi tidak kontinu karena adanya rapat elektron pada sisi), maka kita akan memperoleh ekspresi dari potensial listrik [persamaan (5)] dan juga persamaan untuk menyelesaikan dispersi dari EP [persamaan (7)], sebagai berikut

EP dimodelkan sebagai gelombang yang menjalar pada sisi graphene. Semisal sisi berada pada koordinat x = 0, maka potensial listrik ϕ dan rapat elektron δρ dari EP dapat dimodelkan sebagai berikut,

Di mana ω ̃ adalah frekuensi dari EP, ω_b²=2πD(T)q, D(T) is faktor Drude yang bergantung suhu dan γ_tr laju hamburan dari elektron. Kita bisa lihat dari persamaan (29) bahwa potensial listrik dari EP terlokalisasi di dekat sisi yang merupakan karakteristik dari EP. Dengan menuliskan ω ̃=ω - i/τ_p dan menyelesaikan persamaan (31), maka frekuensi ω dan juga waktu hidup τ_p dari EP dapat diperoleh. Berikut adalah grafik dari dispersi dan juga waktu hidup dari EP untuk beberapa suhu. Grafik (a) menunjukkan frekuensi dari EP (garis solid) sebagai fungsi wavevector (q) untuk suhu 50 K (biru) dan 300 K (merah). Bisa kita lihat, bahwa frekuensi EP linear terhadap wavevector dan juga meningkat seiring meningkatnya suhu. Grafik (b) menunjukkan waktu hidup dari EP sebagai fungsi wavevector dan suhu. Seiring dengan bertambahnya suhu, waktu hidup EP semakin berkurang, karena adanya eksitasi termal dari elektron. Meskipun demikian, EP memiliki waktu hidup yang Panjang dibandingkan dengan plasmon permukaan konvensional pada suhu ruang (300 K). Waktu hidup EP sekitar 3 ps, melebihi waktu hidup plasmon permukaan di graphene (0.5 ps). Inset pada grafik (c) juga menunjukkan bahwa semakin besar frekuensi EP (label pada tiap garis), waktu hidup EP juga semakin meningkat.

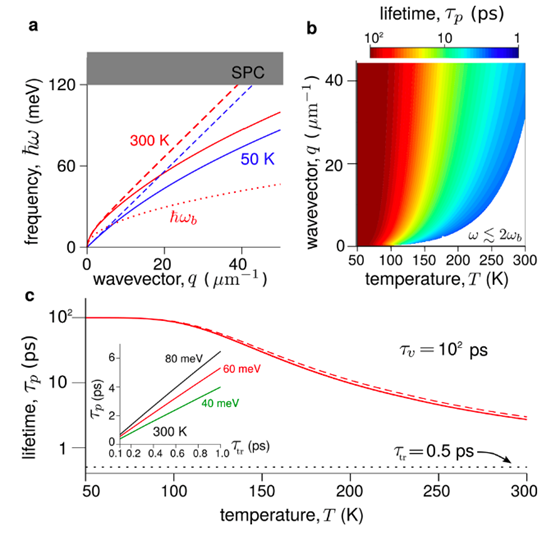
Grafik (c) sendiri menunjukkan bahwa waktu hidup EP untuk ℏω=60 meV menurun seiring meningkatnya suhu dan mencapai 3 ps pada suhu ruang. Panjangnya waktu hidup EP dikarenakan rapat elektron yang hanya terdapat pada edge states saja (karena energi Fermi berada dalam gap energi), sehingga EP tidak dapat meluruh menjadi plasmon permukaan graphene. Peluruhan EP baru muncul saat meningkatnya suhu, karena adanya eksitasi termal yang menyebabkan rapat elektron tidak hanya ada pada edge states saja. Selain panjangnya waktu hidup EP, medan listrik EP lebih terlokalisasi pada permukaan (dan juga batas antara dua region) dibandingkan plasmon permukaan konvensional. Hal ini disebabkan karena panjang gelombang (dan juga kecepatan) EP yang jauh lebih kecil dibandingkan cahaya. Sebagai contoh, panjang gelombang EP sebesar 290 nm untuk ℏω=60 meV, sedangkan panjang gelombang cahaya dengan frekuensi yang sama adalah 20 μm.